Three Dimensional Coordinate Geometry- Coordinate Geomatry- Math

Subject: Matrix and Coordinate Geometry

Subject Code: MATH 4201

Lecturer Name : Mohammad Abu Jabed (MAJ)

Download Link

                    INTRODUCTION TO THREE DIMENSIONAL GEOMETRY

You have read in your earlier lessons that given a point in a plane, it is possible to find two
numbers, called its co-ordinates in the plane. Conversely, given any ordered pair (x, y) there
corresponds a point in the plane whose co-ordinates are (x, y).
Let a rubber ball be dropped vertically in a room The point on the floor, where the ball strikes,
can be uniquely determined with reference to axes, taken along the length and breadth of the
room. However, when the ball bounces back vertically upward, the position of the ball in space
at any moment cannot be determined with reference to two axes considered earlier. At any
instant, the position of ball can be uniquely determined if in addition, we also know the height of
the ball above the floor.
If the height of the ball above the floor is 2.5cm
and the position of the point where it strikes
the ground is given by (5, 4), one way of
describing the position of ball in space is with
the help of these three numbers (5, 4, 2.5).

Thus, the position of a point (or an article) in
space can be uniquely determined with the
help of three numbers. In this lesson, we will
discuss in details about the co-ordinate system
and co-ordinates of a point in space, distance
between two points in space, position of a
point dividing the join of two points in a given
ratio internally/externally and about the
projection of a point/line in space.

OBJECTIVES

After studying this lesson, you will be able to :
● associate a point, in three dimensional space with given triplet and vice versa;
● find the distance between two points in space;
● find the coordinates of a point which divides the line segment joining twogiven points in a given ratio internally and externally;
● define the direction cosines/ratios of a given line in space;
● find the direction cosines of a line in space;
● find the projection of a line segment on another line; and
● find the condition of perpendicularity and parallelism of two lines in space.

EXPECTED BACKGROUND KNOWLEDGE 

● Two dimensional co-ordinate geometry
● Fundamentals of Algebra, Geometry, Trigonometry and vector algebra.

COORDINATE SYSTEM AND COORDINATES OF A POINT IN SPACE

Recall the example of a bouncing ball in a room where one corner of the room was considered
as the origin.
It is not necessary to take a particular
corner of the room as the origin. We couldhave taken any corner of the room (for
the matter any point of the room) as origin

of reference, and relative to that the co-
ordinates of the point change. Thus, the

origin can be taken arbitarily at any point
of the room.
Let us start with an arbitrary point O in
space and draw three mutually
perpendicular lines X'OX, Y'OY and
Z'OZ through O. The point O is called the
origin of the co-ordinate system and the
lines X'OX, Y'OY and Z'OZ are called
the X-axis, the Y-axis and the Z-axis
respectively. The positive direction of the
axes are indicated by arrows on thick lines
in Fig. 33.2. The plane determined by the
X-axis and the Y-axis is called XY-plane
(XOY plane) and similarly, YZ-plane
(YOZ-plane) and ZX-plane (ZOX-plane)
can be determined. These three planes are
called co-ordinate planes. The three
coordinate planes divide the whole spaceinto eight parts called octants.
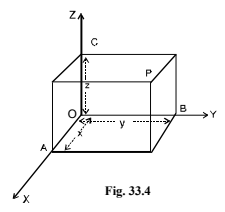
Let P be any point is space. Through P
draw perpendicular PL on XY-plane

meeting this plane at L. Through L draw a line LA
parallel to OY cutting OX in A.
If we write OZ = x,AL = y and LP = z, then (x, y, z) are the co-ordinates of the point P.
Again, if we complete a reactangular parallelopiped
through P with its three edges OA, OB and OC
meeting each other at O and OP as its main diagonal
then the lengths (OA, OB, OC) i.e., (x, y, z) are
called the co-ordinates of the point P.

Note : You may note that in Fig. 33.4
(i) The x co-ordinate of P = OA = the length of perpendicular from P on the YZ-plane.
(ii) The y co-ordinate of P = OB = the length of perpendicular from P on the ZX-plane.
(iii) The x co-ordinate of P = OC = the length of perpendicular from P on the XY-plane.
Thus, the co-ordinates x, y, and z of any point are the perpendicular distances of P from the
three rectangular co-ordinate planes YZ, ZX and XY respectively.
Thus, given a point P in space, to it corresponds a triplet (x, y, z) called the co-ordinates of
the point in space. Conversely, given any triplet (x, y, z), there corresponds a point P in space
whose co-ordinates are (x, y, z).

Remarks

1.  Just as in plane co-ordinate geometry, the co-ordinate axes divide the plane into four quadrants, in three dimentional geometry, the space is divided into eight octants by the co-ordinate planes, namely OXYZ, OX'YZ, OXY'Z, OXYZ', OXY'Z', OX'YZ', OX'Y'Z and OX'Y'Z'.
    
2.  If P be any point in the first octant, there is a point in each of the other octants whose absolute distances from the co-ordinate planes are equal to those of P. If P be (a, b, c), the other points are (-a, b, c), (a, -b, c), (a, b, -c), (a, -b, -c), (-a, b, -c), (-a, -b, c) and (-a, -b, -c) respectively in order in the octants referred in (i).
    
3. The co-ordinates of point in XY-plane, YZ-plane and ZX-plane are of the form (a, b,0), (0, b, c) and (a, 0, c) respectively.
    
4. The co-ordinates of points on X-axis, Y-axis and Z-axis are of the form (a, 0, 0), (0, b,0) and (0,0, c) respectively.
    
5. You may see that (x, y, z) corresponds to the position vector of the point P with reference to the origin O as the vector OP

Example 33.1 

Name the octant wherein the given points lies :

(a) (2, 6, 8) (b) (-1, 2, 3) (c) (-2, -5, 1)
(d) (-3, 1, -2) (e) (-6, -1, -2)

Solution :

(a) Since all the co-ordinates are positive, \ (2, 6, 8) lies in the octant OXYZ.
(b) Since x is negative and y and z are positive, \ (-1, 2, 3) lies in the octant OX'YZ.
(c) Since x and y both are negative and z is positive \(-2, -5, 1) lies in the octant OX'Y'Z.
(d) (-3, 1, -2) lies in octant OX'YZ'.
(e) Since x, y and z are all negative \(-6, -1, -2) lies in the octant OX'Y'Z'.

CHECK YOUR PROGRESS 33.1

1. Name the octant wherein the given points lies :
(a) (-4, 2, 5) (b) (4, 3, -6) (c) (-2, 1, -3)
(d) (1, -1, 1) (f) (8, 9, -10)

33.2 DISTANCE BETWEEN TWO POINTS

Suppose there is an electric plug on a wall of a room
and an electric iron placed on the top of a table. What
is the shortest length of the wire needed to connect the
electric iron to the electric plug ? This is an example
necessitating the finding of the distance between twopoints in space.
Let the co-ordinates of two points P and Q be
( x,y,z 111 ) and ( x222 , y , z ) respectively. With
PQ as diagonal, complete the parallopiped
PMSNRLKQ.
PK is perpendicular to the line KQ.\ From the right-angled
triangle PKQ, right angled at K,
We have 222 PQ = + PK KQ
Again from the right angled triangle PKL right angled
at L,

Example 33.2
Find the distance between the points ( 2, 5, 4 - ) and ( 8, 2, 6 - ).

Solution :
 Let P ( 2, 5, 4 - ) and Q ( 8,2, 6 - ) be the two given points.

The distance between the given points is 7 units.

Example 33.3
Prove that the points ( - - 2, 4, 3 ), ( 4, - - 3, 2 ) and ( - - 3, 2, 4 ) are
the vertices of an equilateral triangle.

Solution :
Let A ( - 2, -4, 3),B( 4,  - 3, -2 ) and C ( -3, -2,4 ) be the three given points.

Since |AB| =  |BC| = |CA| ,  △ ABC is an equilateral triangle.

Example 33.4 
Verify whether the following points form a triangle or not :
(a) A ( -1, 2, 3) B(1, 4, 5) and C( 5, 4, 0)
(b) ( 2, - 3, 3 ), (1, 2, 4 ) and ( 3, - 8, 2 )

Solution :

CHECK YOUR PROGRESS 33.2

1.  Find the distance between the following points :

• (a) ( 4, 3, 6  ) and ( - 2,1, -3) (b) ( - 3,-1, 2 ) and (-3, -1, 2 )  ( c) ( 0, 0, 0) and ( -1,1,1)  

1. Show that if the distance between the points ( 5, - 1, 7 ) and ( a, 5,1) is 9 units, "a" must be either 2 or 8.
2. Show that the triangle formed by the points ( a, b, c ), ( b, c, a ) and ( c, a, b ) is equilateral
3. Show that the the points ( - - 1, 0, 4 ), ( 0,1, 6 - ) and (1, 2, 5 - ) form a right angled tringle.
4. Show that the points ( 0, 7,10 ), ( -1, 6, 6 ) and ( -4, 9, 6 ) are the vertices of an isosceles right-angled triangle.
5. Show that the points ( 3, - 1, 2 ), ( 5, - - 2, 3 ), ( -2, 4,1) and ( -4, 5, 6 ) form a parallelogram. 
6. Show that the points ( 2, 2, 2 ), ( -4, 8, 2 ), ( -2, 10, 10 ) and ( 4, 4, 10 ) form a square.
7. Show that in each of the following cases the three points are collinear :
   (a) ( -3, 2, 4 ), ( -1, 5, 9 ) and (1, 8,14 )
   (b) ( 5, 4, 2), ( 6, 2, 1 - ) and ( 8, - - 2, 7 )
   (c) ( 2, 5, 4 - ), (1, 4, 3 - ) and ( 4, 7, 6 - ) 

COORDINATES OF A POINT OF DIVISION OF A LINE SEGMENT  
 









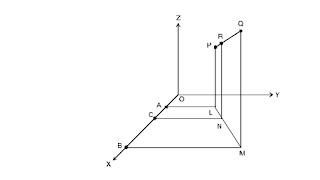
Let the point R (x, y, z) divide PQ in the ratio l : m internally.
Let the co-ordinates of P be ( x1,y1,z1 ) and the co-ordinates of Q be ( x2,y2,z2  ). From
points P, R and Q, draw PL, RN and QM perpendiculars to the XY-plane. 

 To Read More Please Download the full Lecture. 
 
Download Link