Matrix math and Solution - Math

Matrix

Download Link

Solution Download Link

A matrix is a collection of numbers arranged into a fixed number of rows and columns. Usually the numbers are real numbers. In general, matrices can contain complex numbers but we won't see those here.

If the symbol $a_ij$ represents any number, then $\begin{pmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{pmatrix}$ is called a m х n matrix.

This means that the number of rows of the matrix is m and the number of its columns is n

The matrix is also expressed by the following symbol:
$[a_ij ],i=1,2,3-------m; j=1,2,3,------n$

$a_ij$ is called the element of the matrix. The position of the element $a_ij$ is in i-th row and in j-th column

Examples of Matrix:

1. Row Matrix: A matrix having only one row is called a row matrix or a row vector.

$A=[a_11 a_12 a_13……… a_1n ]$ is a row matrix. The number of its row is 1 but the number of its columns is n; so, this is a matrix of order 1 х n.
2. Column Matrix: A matrix having only one column is called a column matrix or a column vector
$\begin{pmatrix} a_{11} & \\ a_{21}\\ a_{31} \end{pmatrix}$ is a column matrix

The number of column of this matrix is 1 but the number of rows is m. So, this is a matrix of order mх1

3. Square matrix: If the number of rows of a matrix and the number of its columns are equal, the matrix is said to be a square matrix.

$\begin{pmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{pmatrix}$ is a square matrix since the number of its rows & columns are both equal to n.

The order of a square matrix consisting of n rows and n columns is n.

The elements a₁₁a₂₂a₃₃ ... ... a_nnof the square matrix are called diagonal elements. The sum of the diagonal elements is called trace.

4. Diagonal Matrix: The square matrix whose elements a_ij = 0 when i キ j, is called a diagonal matrix

D= $\begin{pmatrix} a_{11} & {0} & {0}\\ {0} & a_{22} & {0}\\ {0} & {0} & a_{33} \end{pmatrix}$ is a diagonal matrix.

5. Scalar Matrix: If the non-zero elements of a diagonal matrix are equal, the matrix is called a scalar matrix.
D= $\begin{pmatrix} {a} & {0} & {0}\\ {0} & {a} & {0}\\ {0} & {0} & {a} \end{pmatrix}$ is a scalar matrix.

6. Identity (Unit) Matrix: If the non-zero elements of a scalar matrix are each equal to 1, the matrix is called an identity matrix or unit matrix. Unit matrix of order n is denoted by the symbol In .

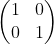
For example, I3 = $\begin{pmatrix} {1} & {0} & {0}\\ {0} & {1} & {0}\\ {0} & {0} & {1} \end{pmatrix}$ , I2 = $\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$

7. Zero (Null) Matrix: In a Zero matrix all the elements of its rows and columns are zero
A= $\begin{pmatrix} {0} & {0} &{0}\\ {0} & {0} & {0}\\ {0} & {0} & {0} \end{pmatrix}$ is a Zero Matrix.

Mechanical

Header Ads

Matrix math and Solution - Math

No comments

Popular

Recent

Comments

Categories

Tags

About Me

Lectures

Popular Posts